ある程度知識を前提にしていますが、なくてもワンチャンいけます。
削除の解説
葉ノードは省略して簡単な形で書いています。
その1(削除したら空エントリが発生する&「2度手間」も発生するパターン)
具体例を通して解説します。
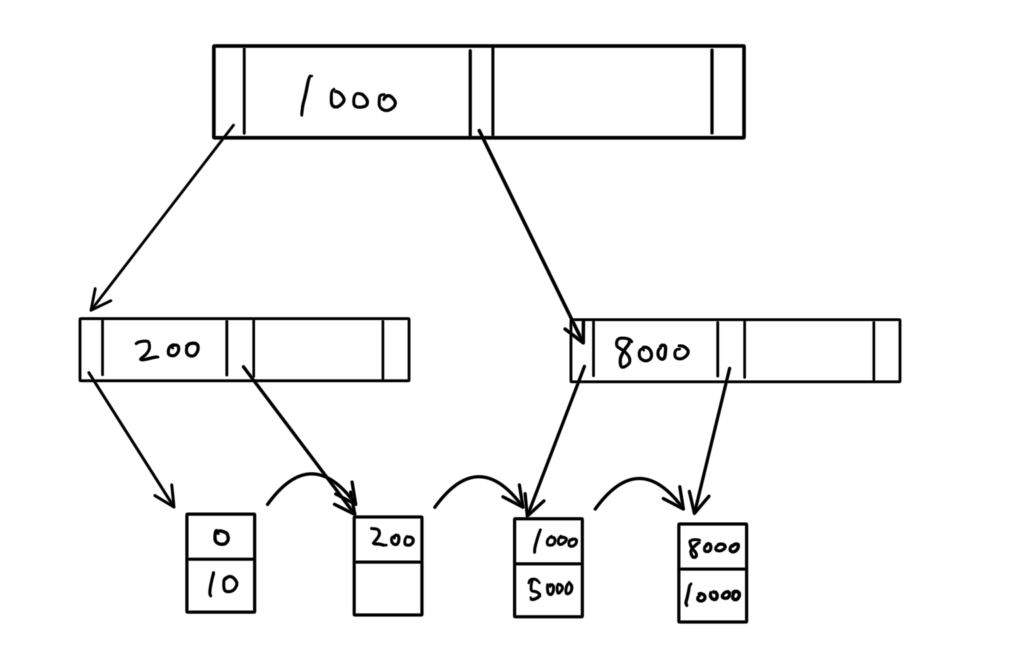
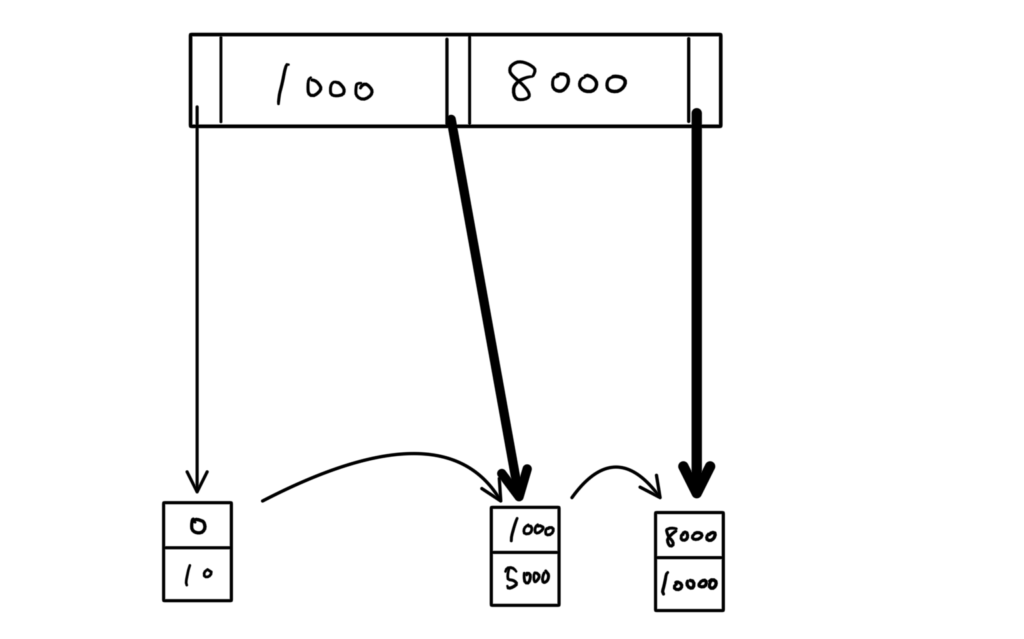
ここから「200」を削除するステップを見ていく。
一般論 中身が空のエントリと、空エントリを指すポインタは存在してはいけない。
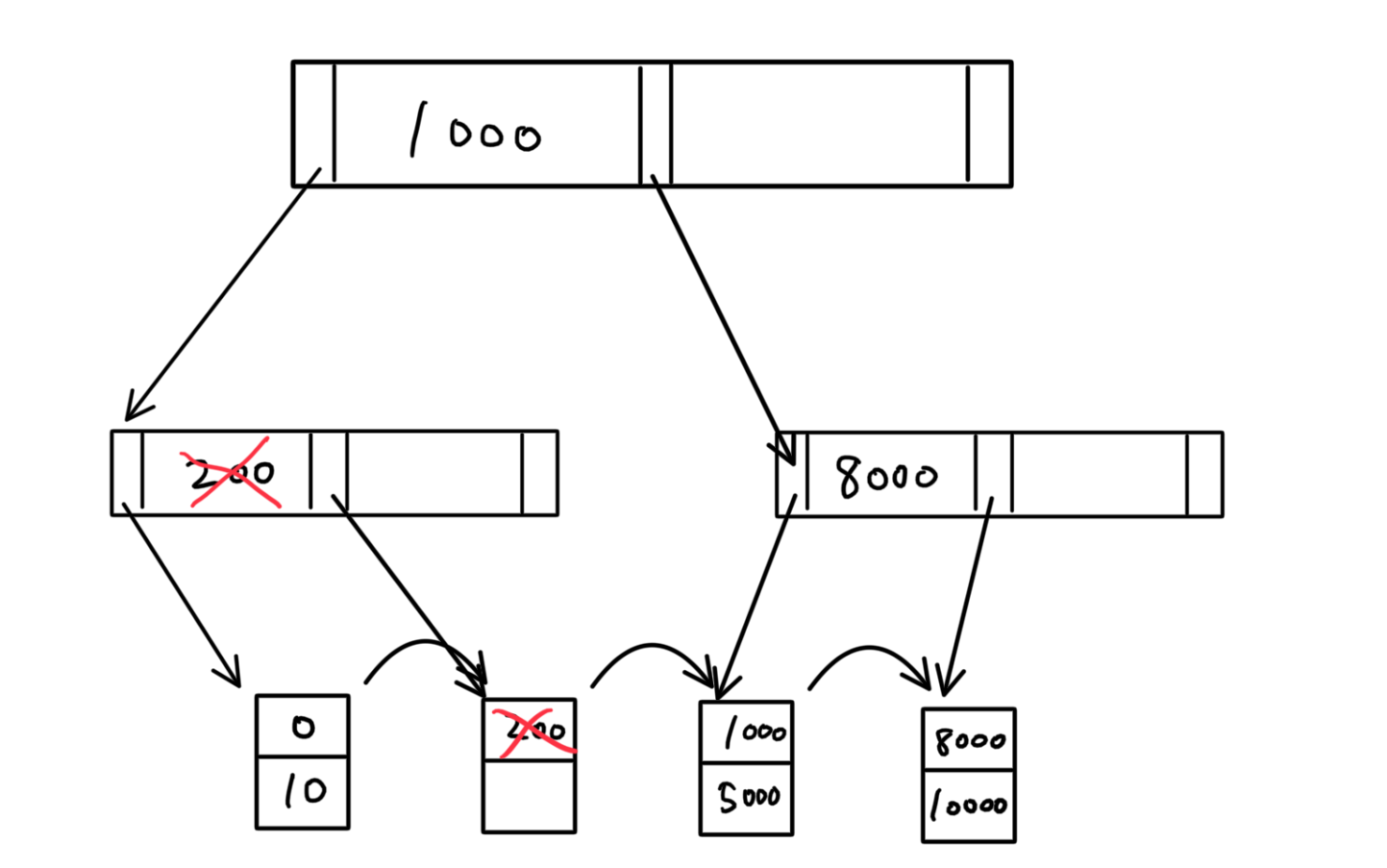
値の削除に伴って、不要になるポインタ(矢印)も削除する。(青色のバツで表した)
そして、新しく必要になるポインタを青の矢印で表す。
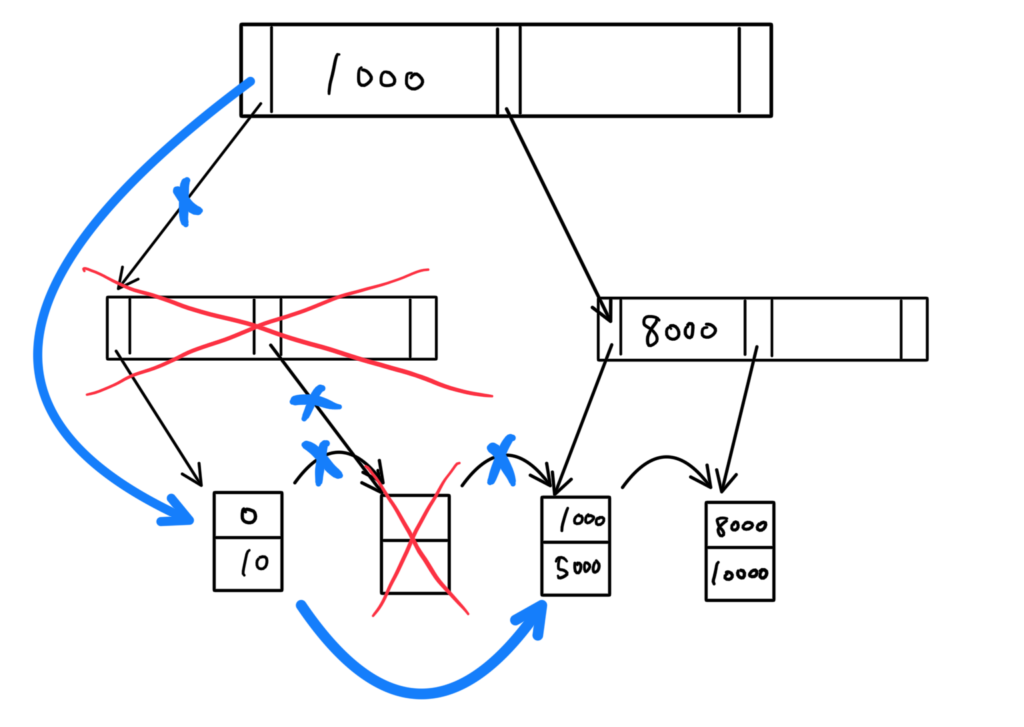
実際に書き直すと、
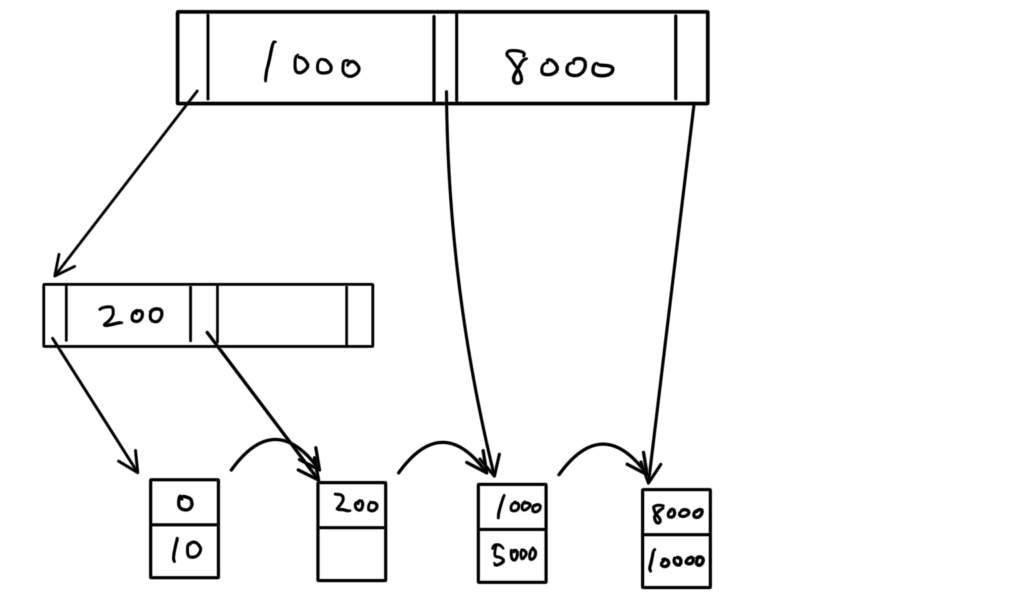
2度手間になっている部分(根→値「8000」を含むノード→葉 の部分)がある。
半透明の青の矢印で繋げば、2度手間が回避できる。(根→葉 で済む)
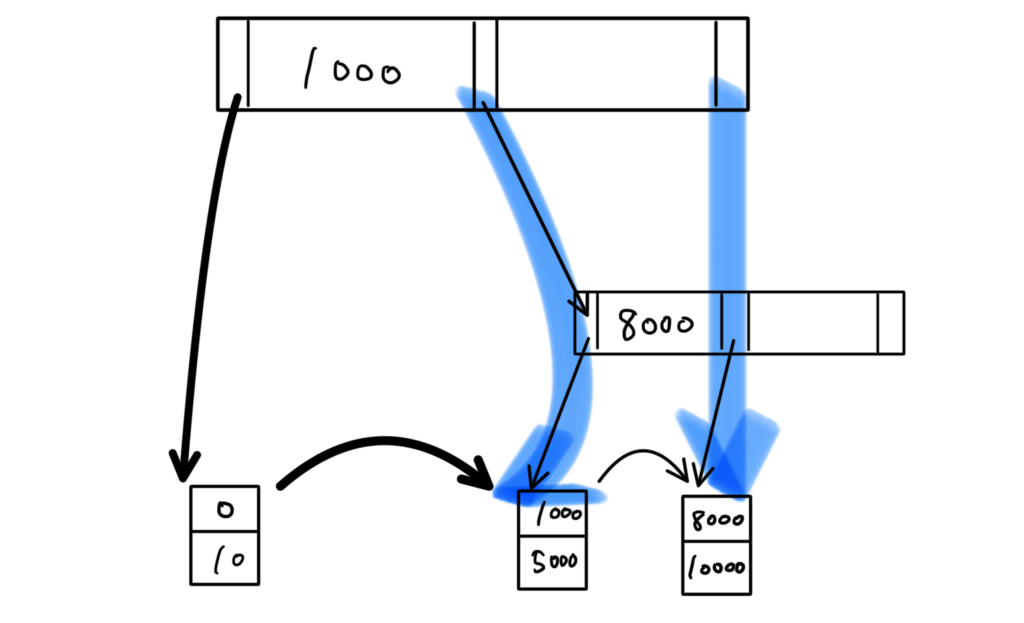
つまり、「上から2つ目の8000」が不要になる。
一般論 削除の操作をした際に、このように、2度手間になったエントリ(四角)を省く操作をする
実際に書き直すと、
完成。
おまけ

この時点で上から2番目の「8000」も「2度手間」になっていて、消せそうに思えるが、それはできない。
と書くのは、B+木の定義に反するからだ。
一般論 根(一番上のノード)から葉(最下層のノード)までの距離は一定。
今回なら、
左から一番目と二番目の葉ノードは「根から葉までの距離」が2であり、
左から三番目と四番目の葉ノードは「根から葉までの距離」が1であるので、
定義に反する。
その2(その1と同じだが、再帰的な操作が必要なパターン)
操作が1回でなく、削除や挿入を2回、3回、、、と繰り返すしてB+木が完成するパターンもある。
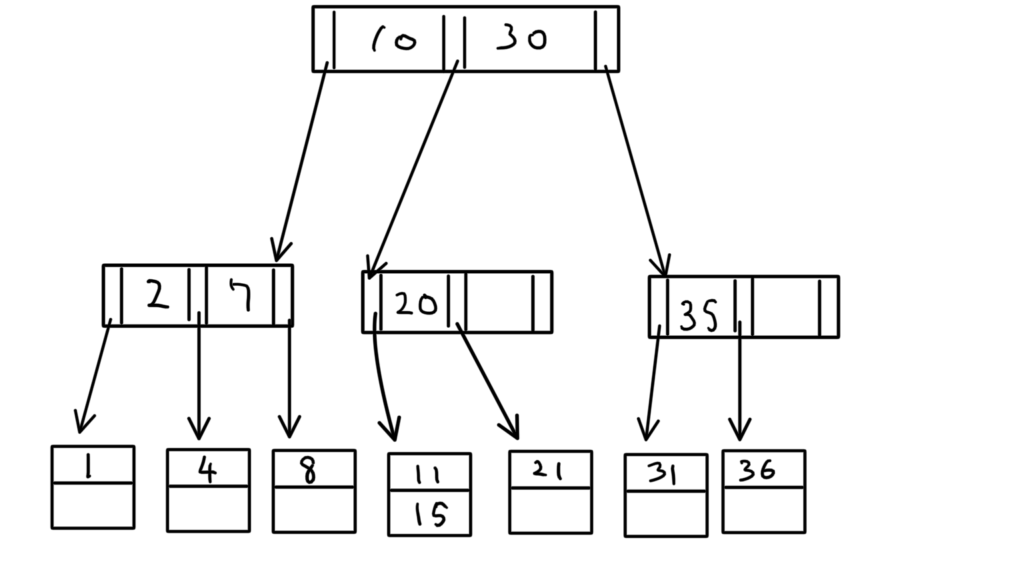
葉ノード間のポインタは省略した。
「11」と「21」を削除すると、
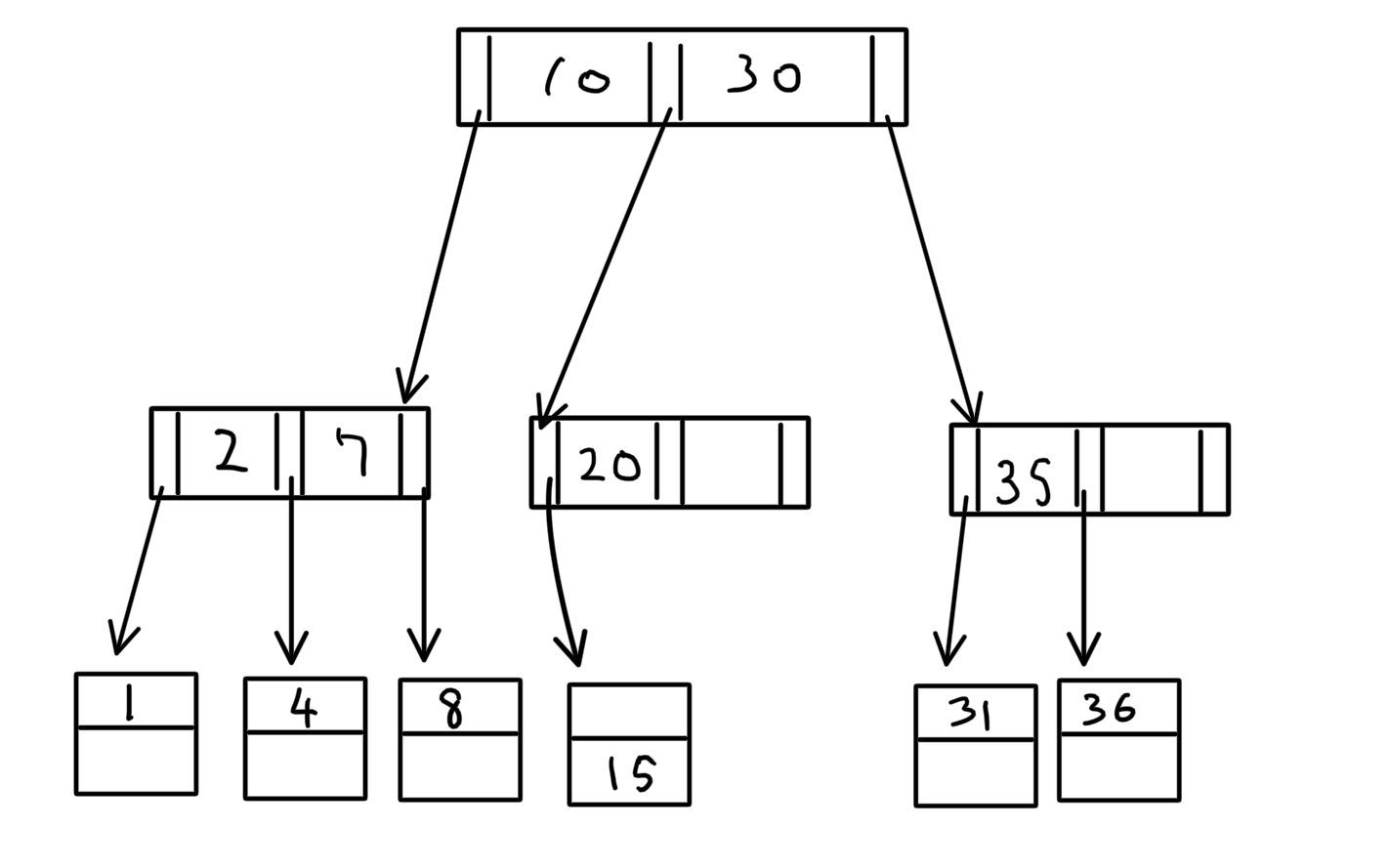
このままでは、B+木の定義に反する。

一般論 葉ノード以外のノードは値(探索キー)を1つは持つので、ポインタは最低でも2つはもつ。 ※B+木のオーダが1の時のみ成り立つ。 「最後に」の部分に少し書いた。
つまり、「赤モコモコ」の部分がないので、定義に反する。
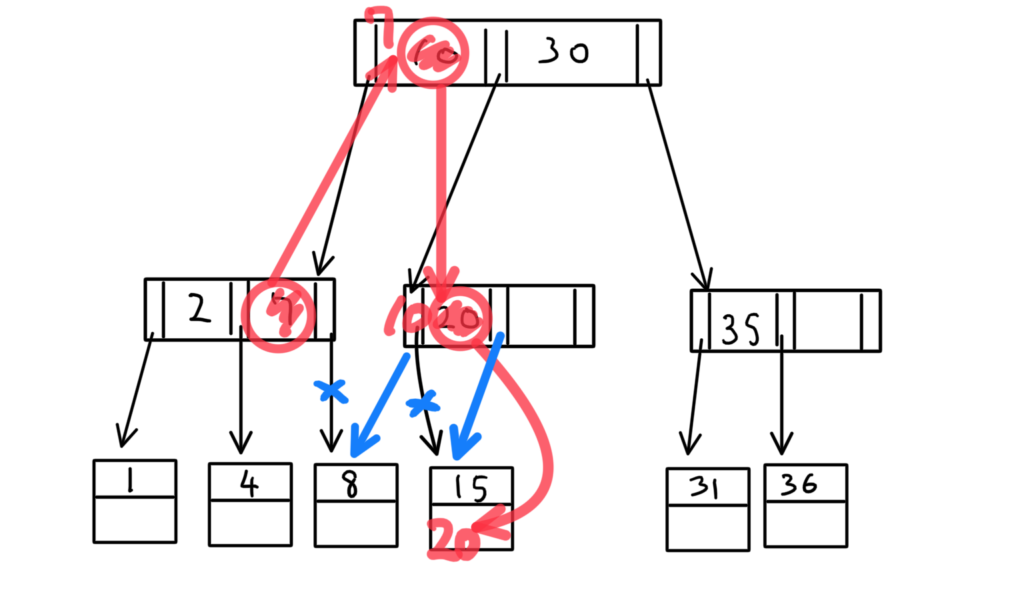
適当に中間ノード(根と葉以外)から値を持ってきてB+木を修正する。
(具体的には、「10」削除。「10」を「20」の位置に挿入。)
色付きの部分を書き直すと、
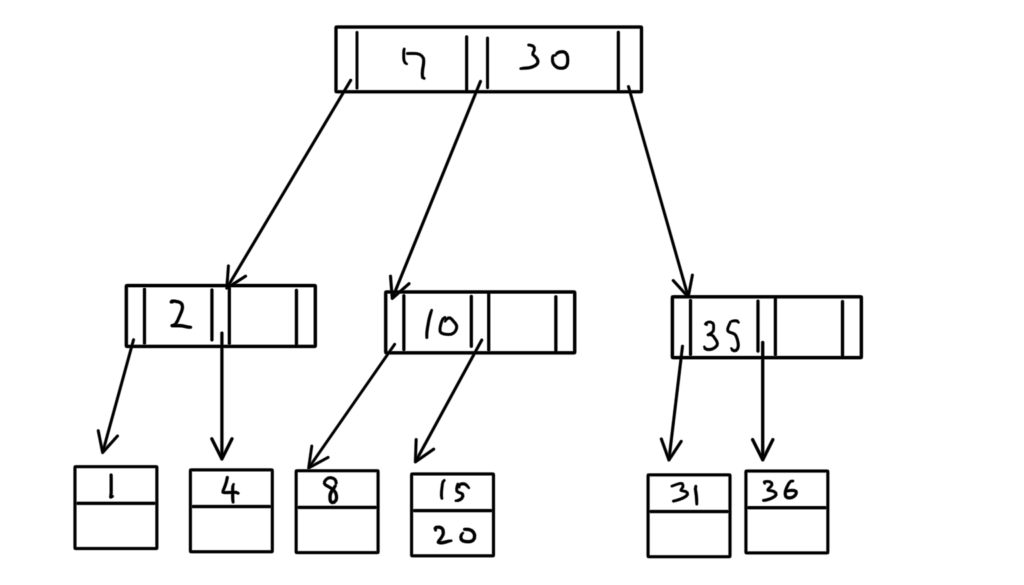
完了。
その3(削除したら空エントリが発生する&「2度手間」が発生しないパターン)
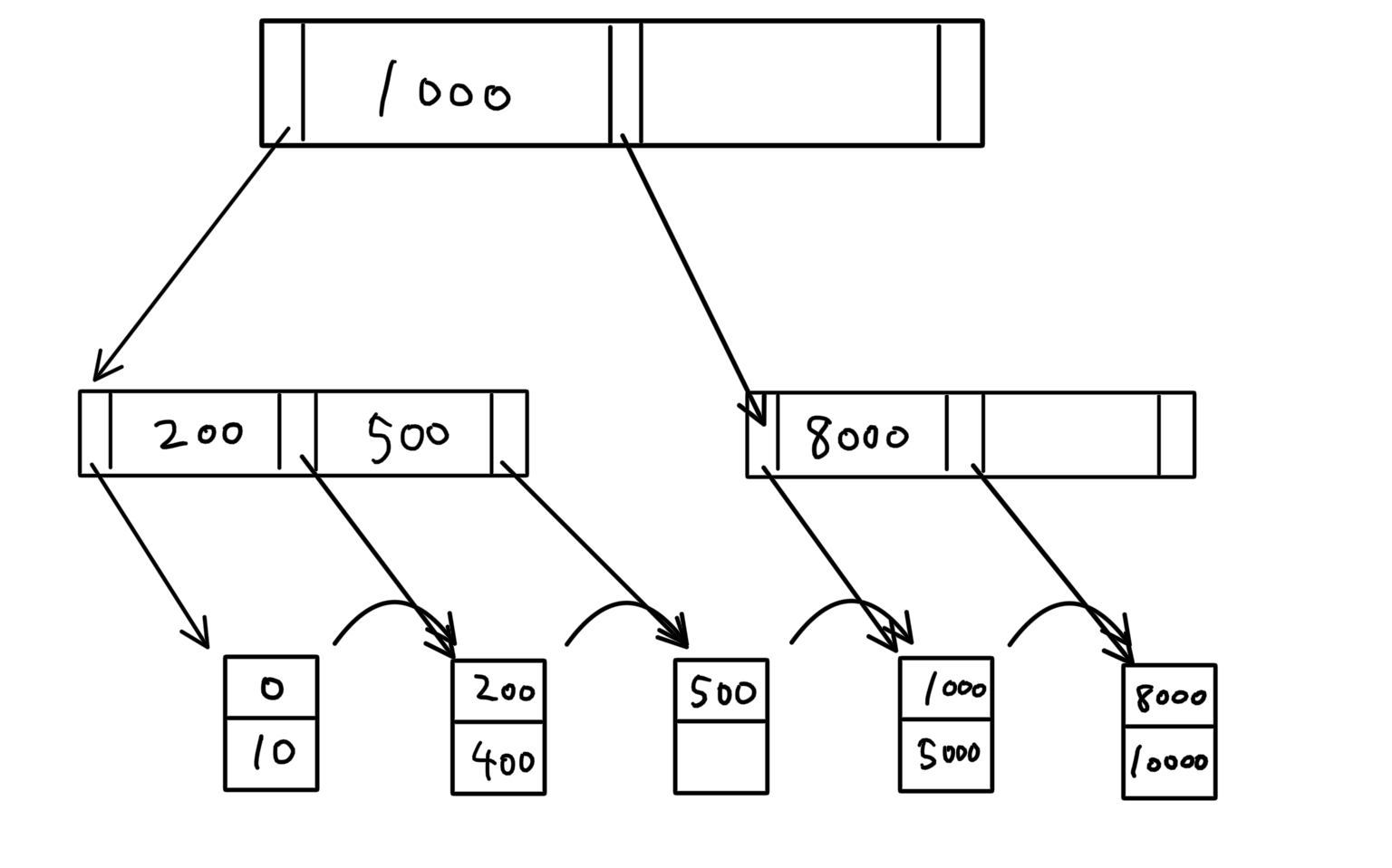
「500」を削除すると、
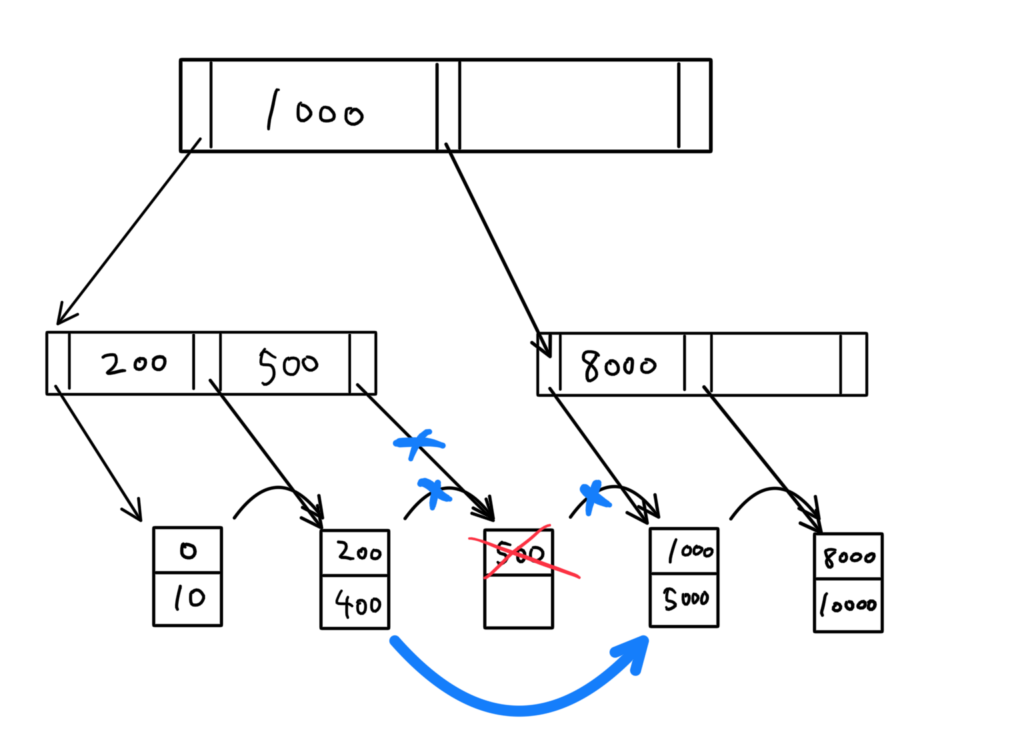
書き直すと以下のようになる。
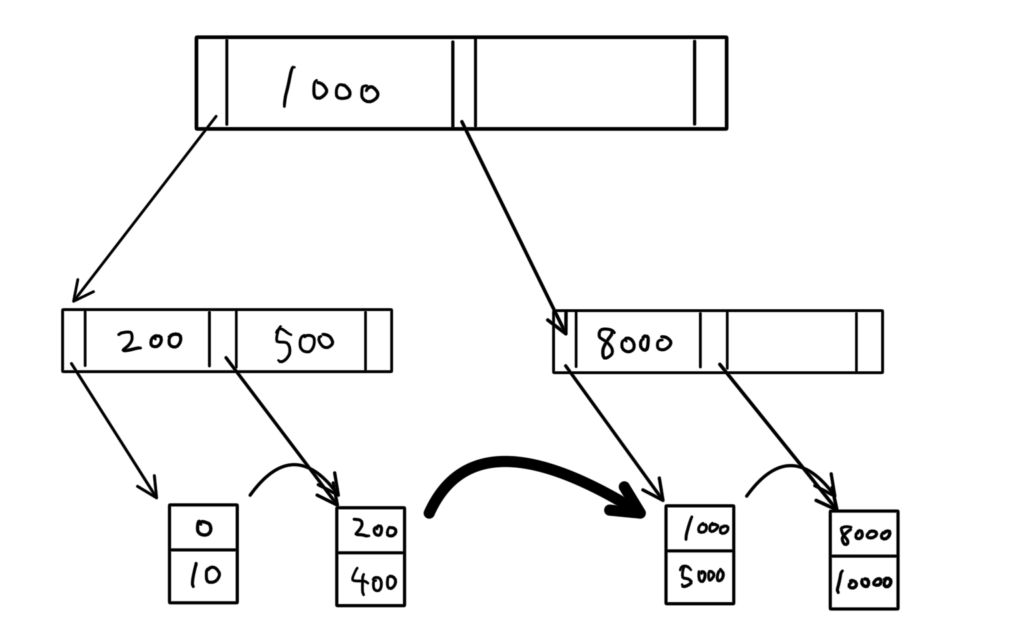
完了。
その4(削除しても空エントリが発生しないパターン)
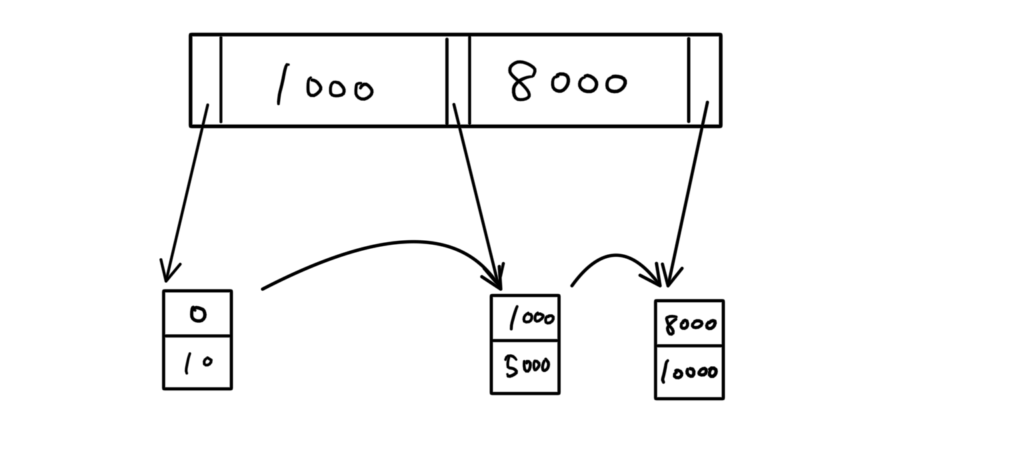
「5000」を削除すると、
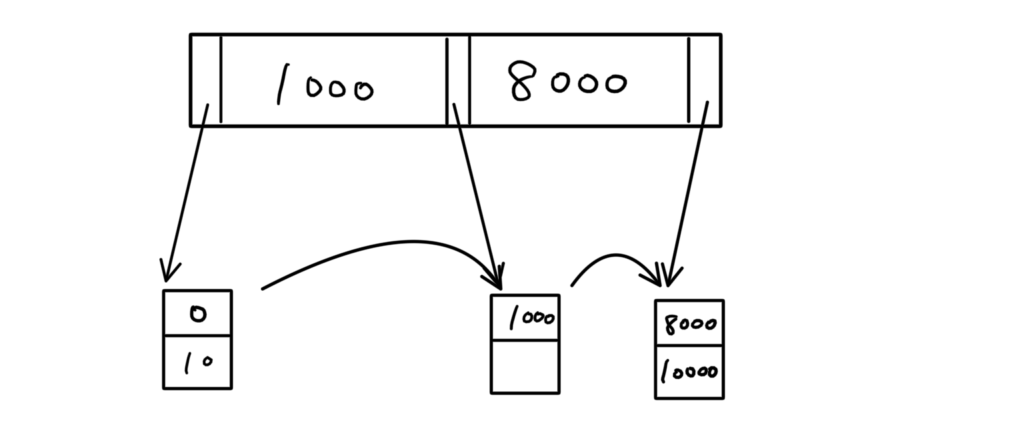
完了。
おまけ
もっと簡単に省略できるとしても、削除して空になったセルがない場合は、B+木の構造はそのままです。
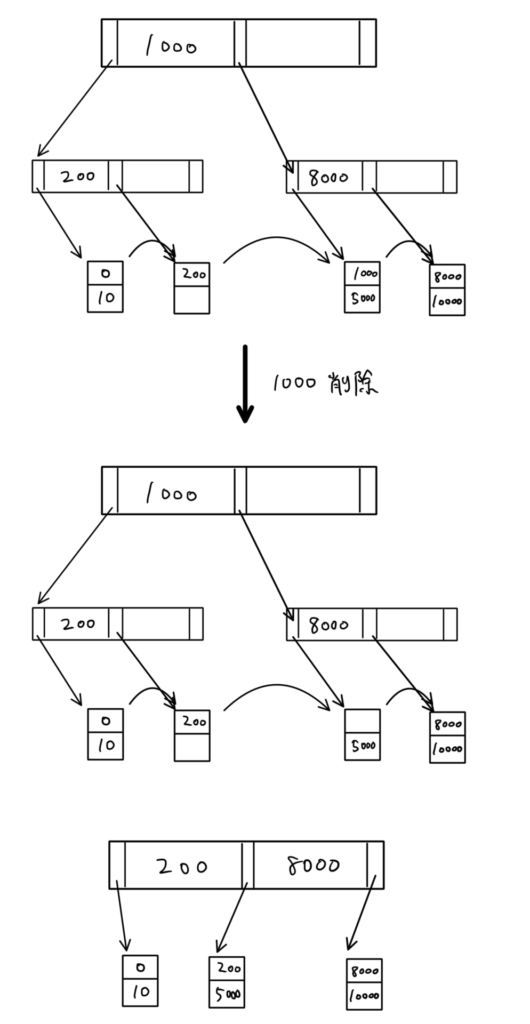
このように変形できそうですが、

ここの「赤モコモコ」が空エントリでないので、この時点で完了しています。
挿入の解説
その1(挿入先が満タンのパターン)
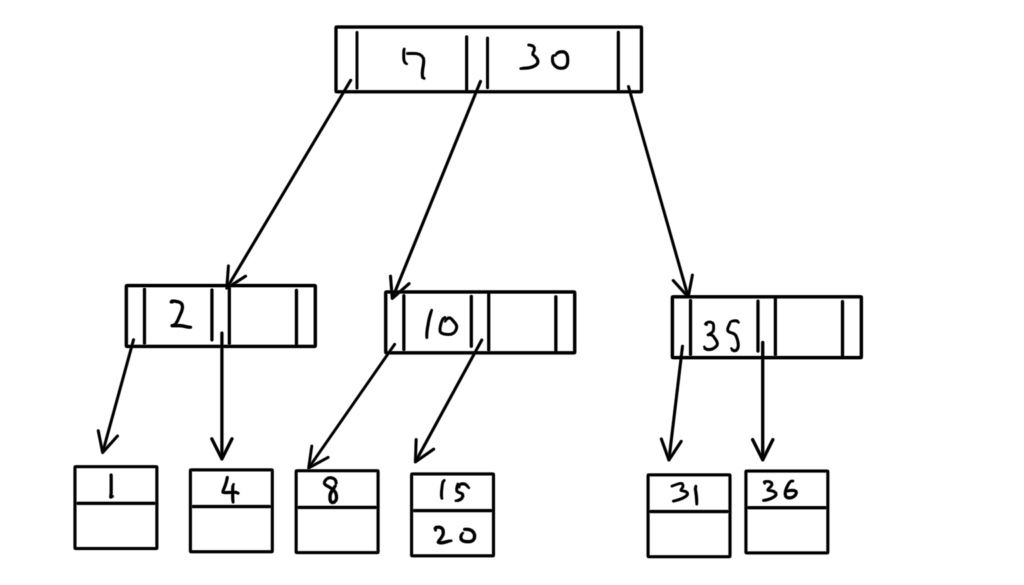
ここに「16」を挿入すると、
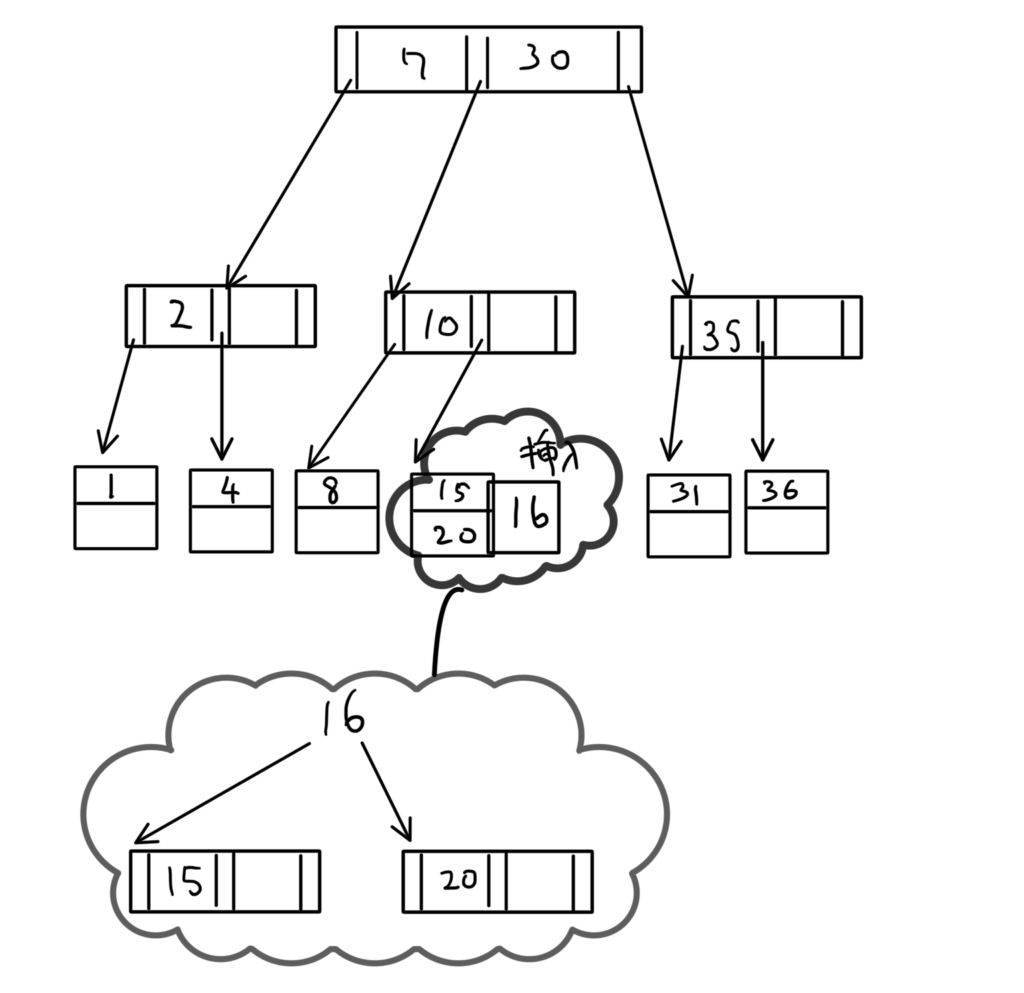
挿入先のエントリに3つも値があることになるが、今回はエントリが2つまでしか値を持てないB+木を考えているので、「下のモコモコ」のように分けて考える。(「16」を四角で囲んでいないのは、「とりあえず15と20の上にある値」ってイメージで書いているだけです。)
しかし、「下のモコモコ」に交換すると、
一般論 根(一番上のノード)から葉(最下層のノード)までの距離は一定。
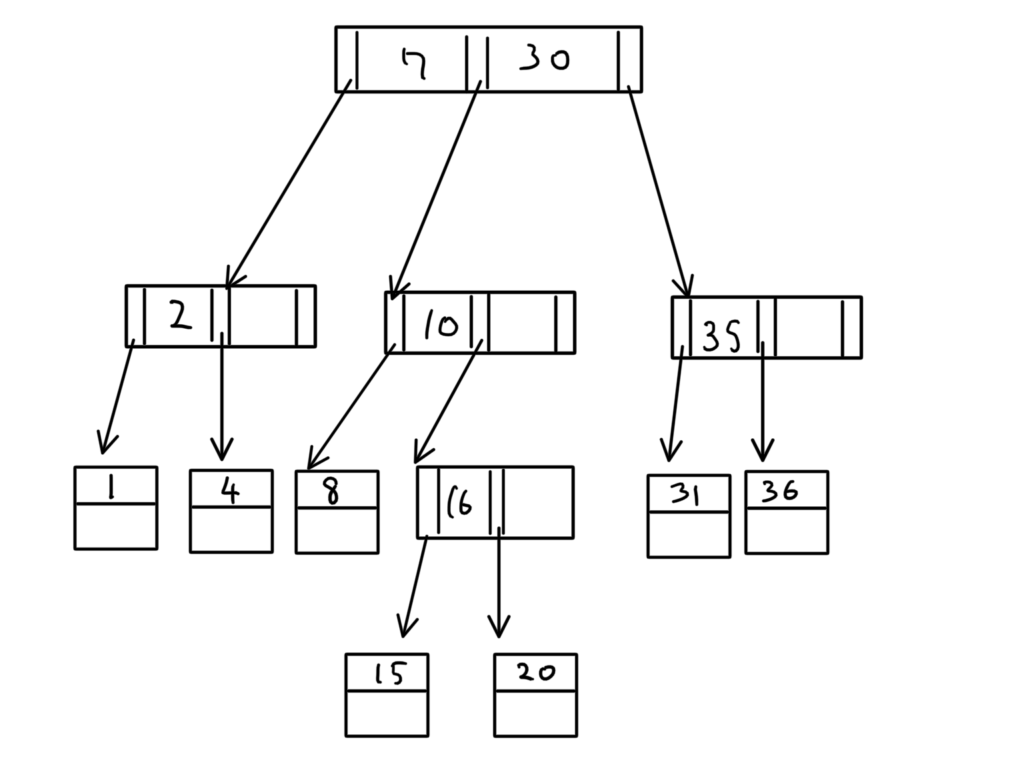
これに反するので、修正すると、
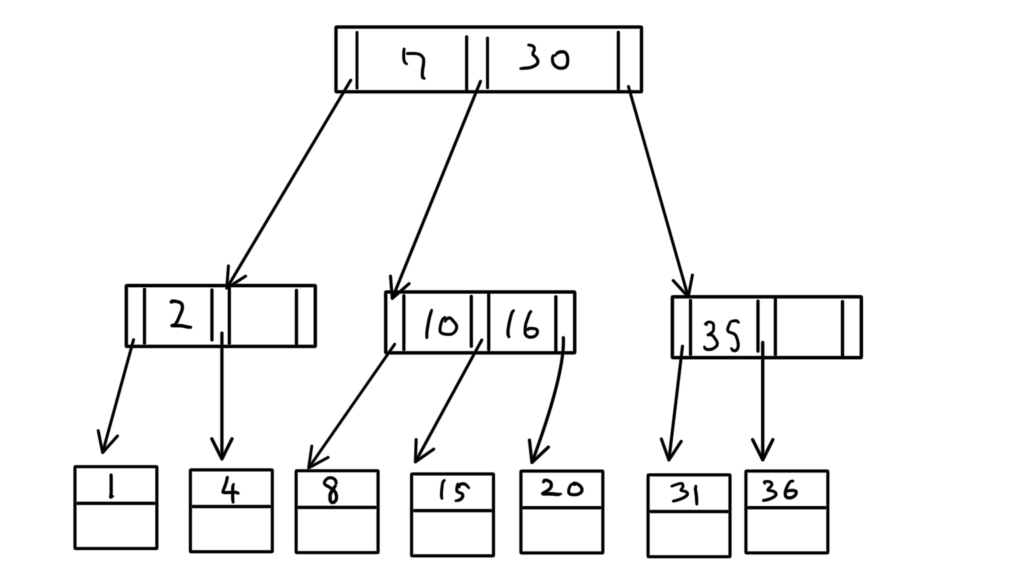
定義を満たすB+木が完成した。
完了。
その2(挿入先に空きがあるパターン)
もうお察しだとは思いますが、
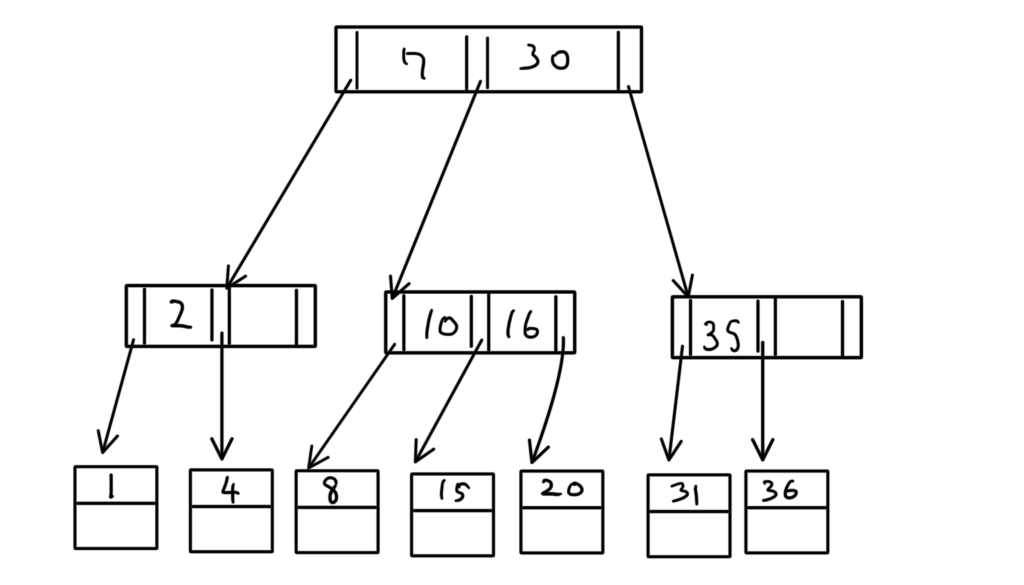
ここに「21」を挿入すると、
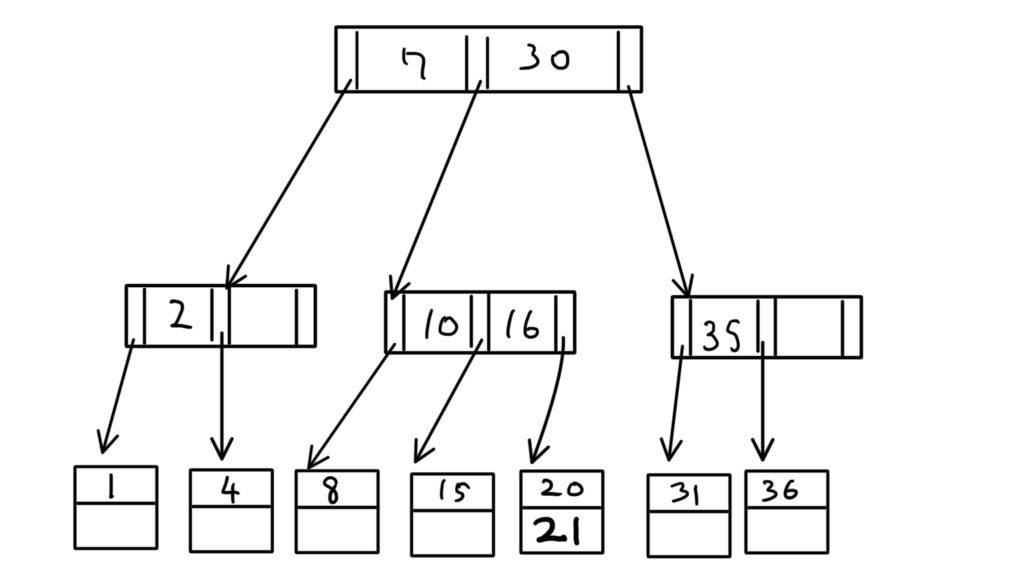
完了。
最後に
以上の解説は全て、B+木のオーダはm=1としています。
・m>1の場合も同様
・どの本や記事でもm=1の場合で書いていた
・m=1の方が見やすい
ので、m=1で図解を作りました。
なので、「その2」で出てきた部分は、正確には、↓のようになります。
一般論 葉でも根でもないノードはm個以上の値(探索キー)を持つので、ポインタは最低でもm+1個ある。
一般論 根ノードは1個以上の値(探索キー)を持つので、ポインタは最低でも2つある。
〜〜以下、雑談なので読まなくてokです〜〜
大学のPDFとかIT系の記事は既にありました(2022/8)が、内容・表現が近いものが多く、「それはさっきの記事で読んだけど、そこじゃない部分が見たいんだよな〜」って感じだったり、参考書を見ても「ん〜、厳密すぎて分かりにくいな〜」って感じだったので、思い切って前提知識を飛ばして尖った記事にしてみました。デカい会社とかじゃないブログならではかなって。映像なら分かりやすいかもなんですけど、ちゃんと詳しい系だと2時間の講義とかだったので、自分のみたい部分探すの億劫ですよね。








コメント