歴史的にAI(人工知能)を実現しようと色々な試みがありました。
最近は機械学習によって特定のタスクに関しては人間平均以上の結果を出すAIが生まれてきたわけです。
機械学習は大きく「教師付き学習」「教師なし学習」「強化学習」に分かれます。
教師付き学習
教師付き学習を行うには「何を学習するか」と「どうやってデータを用意するか」が重要になってきます。
何を学習するか
正解のラベルが付いたデータ(教師)を大量に入力し、未学習かつ類似のデータを正しくラベリングできるように識別関数の重みを学習する。
どうやってデータを用意するか
例えば動物の種類を画像をもとに分類するアルゴリズムを作るなら、大量の動物の画像に犬や猫といったラベルをつけて正解データ(教師。学習データ)を用意し、それを学習させる。
学習後にどれくらいの精度で予想ができるようになったか調べるので、正解データ(教師)とは別に、評価データ(テスト。答え合わせ。)も用意する必要がある。このようにデータを分割して検証する方法を交差検証法(クロスバリエーション)と呼ぶ。
教師付き学習の活用例
・スパムメール(迷惑メール)かどうかを自動判定
・新築の物件の販売価格を、過去の販売価格に基づいて予想
教師なし学習
正解データは使わない。データそのものの特徴やルールを自ら見つけ出す。
例えば、大量のメールを分類するだけ分類して、人がその分類を見て、「このクラスは、迷惑メールだな」「こっちは仕事のメールだな」と解釈する。
ネットのpersonalized広告(その人向けの広告を自動で表示させるやつ)も教師なし学習です。筋トレ記事の検索してる→プロテイン買ってる、引っ越し調べてる→家電買ってる、みたいなデータをたくさん集めてクラスタリング(分類)すれば、それだけで良いからですね。次から、筋トレ記事を見ている人にプロテインの広告を出すだけなので、人の介入は必要ないですね。(メールだと、最初に「迷惑メール」をいう名前を付けるとこだけ人が介入する)
ちなみに、厳密に言うと
クラスタリング→データの属性が不明で、共通の特徴を見出してグルーピングする(=教師なし学習)
分類→既にデータの属性がわかっていて、新しい未知のデータの属性が、既存のどれに当てはまるか予想する(=教師あり学習)
であり、違う用語です。
強化学習
強化学習を行う場合は「何を学習するか」「どうやって試行するか」が重要になってきます。
まず、イメージから見てみましょう。
1日でできるだけ遠くに自転車で行きたい人がいたとする。
サイクリスト(エージェント)はペダルを漕いだり休んだりする(行動)。
そうすると、路面の状況や走行速度(状態)が変化し、ある程度時間が経てば走行距離(報酬)が分かります。今回は1日でできるだけ遠くに行くことが目的なので、長い距離を走れば走るほど報酬(即時報酬ともいう)を多くする(識別関数を調節)でしょう。注意したいのは、強化学習では、最終的にはこの報酬(短期間にもらえる即時報酬)でなく、長い目(今回だと1日)で見た時の価値を最大化するのがゴールです。価値でなく報酬を最大化するのを目的にすると全力で漕ぎまくってすぐバテちゃいそう。
何を学習するか
ある環境(強化学習のモデル)下において、エージェント(学習主体)が何か行動をすると、エージェントの周りの状態が変化し報酬がもらえる。エージェントは一連の行動で報酬が最大になるような方策を学習する。
どうやって試行するか
ある環境(強化学習のモデル)下において、エージェント(学習主体)が何か行動すると、その環境下におけるエージェントの周りの状態が変化し、その結果が報酬としてエージェントにフェードバックする。エージェントは報酬をもとに行動の方策を修正し、また何か行動を起こす。
方策や行動価値関数(ある状態における行動の評価値を出力する関数。Q関数などがある。)が、この報酬を最大化するようになるまで学習を繰り返していく。
強化学習の課題
Q値に基づくアルゴリズムでは「状態行動空間の爆発」と呼ばれる問題が起こりうる。
状態や行動が連続値で定義され、その次元もとても大きい環境だと、状態と行動によって決まるQ値を保存するためには、めちゃめちゃ領域が必要になりパンクします。
解決策として、例えば、AlphaGoではQ値を直接計算せずに、ニューラルネットワークによって近似することによって対処しています。このアイディア自体は昔からあったけど、実際あまり上手く行ってなかったそうです。
強化学習の活用事例
AlphaGo
Googleの関連会社のディープマインド社が開発したコンピュータ囲碁プログラム。
AlphaZERO
同じくディープマインド社が開発したAI。囲碁、将棋、チェスの3つとも、自己学習によって高い学習成果を出した。
自動運転
自動運転にも強化学習アルゴリズムは用いられている。
他の車や人などを検知してエンジン制御などをする。日本国内でも実証実験が増えてきている。
通信ネットワーク経路の最適化
音声データや映像データをそれぞれのデータ特性に応じてトラフィックを最適化する強化学習を用いて、データ移動の遅延を最小にしようとしている。
パーセプトロン(機械学習の元祖)
パーセプトロンとは、ニューラルネットワークの一種であり、機械学習の元祖です。
入力するデータが、例えばアヤメの花の画像なら、花びらの長さ・幅、がくの長さ・幅を測定することにします。そして、x軸が「がくの長さ+幅」、y軸が「花びらの長さ+幅」としてプロットすると2つのクラスに分かれるそうです。
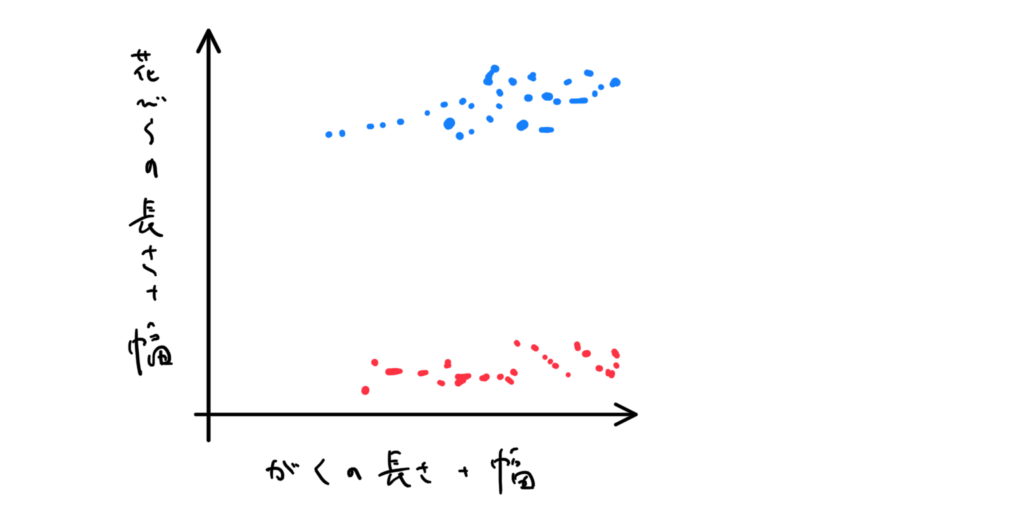
人間なら「あ、この辺に線引けば、いい感じの境界線になるな」と分かりますが、機械学習では、テキトーにデタラメな線から始めて、誤差を修正していくようにします。
そして、この決定境界が引くことができれば学習は完了です。
このような簡単な場合なら単純パーセプトロンという、「入力」と「重みの計算」(誤差調節)の2層のみからなるネットワークでも対応できますが、2つのクラスが重なってる場合や、3クラス以上ある場合は3層以上ある多層パーセプトロンを用います。
多層パーセプトロンのような、多層のニューラルネットワークを深層学習(ディープラーニング)と呼びます。
Q学習(強化学習の1つ)の準備
Q学習はQ値を最大化するように学習するアルゴリズムのこと。
用語などを色々導入しながら強化学習の一般的な話を見ていきます。
エピソード
与えられた環境に対する行動の開始から終了までの期間を1エピソードと呼ぶ。
Q値(状態行動価値)
初期値は0。
ある状態において、ある行動をとった場合の価値。
短期的な報酬でなく、長期的な意味での価値を値として持っている関数(簡単に言うと、価値を表す関数)。
どれくらい長期的にするかは割引率 γ ∈(0,1)で決める。1に近いほど長期的、0に近いほど短期的になる。(将来の不確定要素の分をγで割引きしているイメージ)
t回目の報酬をrtとすると、t回目以降の総報酬Rtは
\begin{aligned}
R_{t}=t_{t+1}+\gamma t_{t+2}+\gamma ^{2}r_{t+3}\
+\ldots =\sum ^{\infty }{k=1}\gamma ^{k+1}r_{t+k}\
\end{aligned}
モデルフリー
強化学習は環境モデル(状態遷移と報酬を予想する関数)を使う(学習する)かどうかで分類する。
環境モデルを使用しないアルゴリズムをモデルフリー、するアルゴリズムをモデルベースと呼ぶ。
モデルフリーの方が実装や調節が容易。今はこっちの方が人気がある。
方策(policy)
選択肢が複数あって、その中からどれを選ぶかを決める基準。
状況sの時に、エージェントが行動aを選択する確率分布π(s,a)を方策と呼ぶ場合もある。
ちなみに今回の方策は
\(\pi \left( s,a\right) =\begin{cases}1\left( a=\arg\max_{a}Q\left( s,a\right) \right) \\0(otharwise)\end{cases}\)
状態価値関数Vπ(s)
状態がsであるときに、エージェントが受け取る総報酬の期待値。
\(V^{\pi}\left( s\right) =E_{\pi } \{R_t| s_t= s\}\)
行動価値関数Qπ(s,a)
状態がsで行動aをとった場合に、エージェントが受け取る総報酬の期待値。
\(Q^{\pi }\left( s,a\right) :=E_{\pi }{ R_{t}| s_{t}=s,a_{t}= a}\)
総報酬Rtの定義より、Vπ(s)とQπ(s,a)の間に次の関係(Bellman方程式)が成立する。
\begin{aligned}
V^{\pi }\left( s\right) =\sum_{a}\pi \left( s,a\right) Q^{\pi }\left( s,a\right) \\
Q^{\pi }\left( s,a\right) =\sum_{s’}P_{s,s’}^{a}\left( R_{s.s’}^{a}+\gamma V^{\pi }\left( s’\right) \right)
\end{aligned}
ここで、\(P^a_{s,s’}\)は状態sで行動aをとった時に状態s’に遷移する確率で、\(R^a_{s,s’}\)は状態sで行動aをとった時の報酬の期待値。
この時、最大の状態価値関数・行動価値関数を達成する方策π*が存在することが証明されている。
最大の状態価値関数・行動価値関数をそれぞれV*(=Vπ*),Q*(=Qπ*)とすると、次の関係(Bellman最適方程式)が成り立つ。
\begin{aligned}
V^{\ast }\left( s\right) =\max_{a}Q^{\ast }\left( s,a\right) \\
Q^{\ast }\left( s,a\right) =\sum_{s’}p_{s,s}^{a},\left( R_{s,s}^{a},+\gamma V^{\ast }\left( 5\right) \right)
\end{aligned}
最善のエージェントを求めること(強化学習のゴール)は、数学的に言うとBellman最適方程式を解くことだったんですね。
これでやっとQ学習の話が始まります。(土下座)
Q学習
Bellman最適方程式の解法にはモンテカルロ法・時間差学習などがあり、Q学習は時間差学習の1つだ。(モンテカルロ法でもQ値を更新するが、更新の仕方が違う。)(あと、資料によっては時間差学習∈Q学習 って書いてるのもあったけど、多分Q学習∈時間差学習で良いはず)
モデル(状態遷移と報酬を予想する関数)に関する情報(\(P^a_{s,s’}\)と\(R^a_{s,s’}\))が不要で、行動1回ごとに価値関数を更新できる。
Q関数はその名の通り行動価値関数Qを更新する。
状態stで行動atを取り、報酬rt+1をゲットし、状態がst+1に遷移した時、Qの値を次のように更新する。
ちなみに、更新していくQが局所に偏らないように、行動atは少しランダム性を加えて選ぶ(ε-greedy法など)。(割といいQ値に更新された後に、もっといい選択肢があるかもしれないのに、同じ値を選び続けてしまう場合がある。ランダム性があるとこれを防げる。人間もそうかも、、)
\begin{aligned}
Q\left( s_{t},a_{t}\right) \leftarrow Q\left( s_{t},a_{t}\right) \
+\alpha( r_{t+1}+\gamma \max {a}Q\left( s_{t+1},a\right) \
-Q\left( s_{t},a_t\right) )
\end{aligned}
ここで、αは学習率と言って、1回の学習でニューラルネットワーク内の重みやバイアスを更新する量の調整値。
これを式変形すると次のようになる。
\begin{aligned}
Q\left( s_{t},a_{t}\right) \leftarrow \left( 1-\alpha\right) Q\left( s_{t},a_{t}\right) \
+\alpha \left( r_{t+1}+\gamma \max {a}Q\left( s_{t+1},a\right) \right) \end{aligned}
更新するたびに\(Q\left( s_{t},a_{t}\right)\)の値が\(\left( r_{t+1}+\gamma \max_{a}Q\left( s_{t+1},a\right)\right)\)にαの割合で近づくことを意味している。
\(r_{t+1}+\gamma \max_aQ\left( s_{t+1},a\right)\)はBelleman最適方程式の中に現れる\(R_{s,s’}^{a}+\gamma V^{\ast }\left( s’\right)\)に対応しており、更新するたびにQはQ*に近づいていく。
関連用語
ε-greedy法
確率εで環境の探索を行い、経験を重ね、探索以外では経験を活用して高い報酬を得られるようにするという方法。εが0.1位でよく上手くいくらしい。
行動に対する反応を広く確認する様からgreedy(貪欲)と名付けられたそうだ。
価値ベースの手法と方策ベースの手法
先ほどのQ学習は価値ベースでした。
名前がややこしいですが、これらはどちらも方策を学習する方法です。
価値ベースの手法
価値関数Qを時間差学習などで学習し、その関数のもので最適な行動を決める。
行動は決定論(あらゆる物事はそれまでの外的要因によって決定する、という考え方。)的になりやすい。(状況に依存して行動が決まりますよね)
価値関数はゴールから逆算して、1つ前の状態、それのさらに1つ前の状態、、、、、のような敷かれたレールが選択されるように報酬を与える。
方策ベースの手法
方策の条件付き確率πを方策勾配法などによって学習し、価値関数を求めずに直接方策を決定する。条件付き確率は、早くゴールした時の行動は重要だと考える(ようになっている)ので、その行動を今後多く取り入れるようになる。行動の選択は確率論的になる。(確率に基づいて行動しているだけですよね)
方策ベース(確率で頑張るやつ)の良い点
・価値ベースでは、各状態に対する役に立たないかもしれない行動に関する値がめっちゃあるが、方策ベースなら最適な方策を直接推定できる。
・行動が連続的な場合と相性が良い
・価値ベースはその時の状況に基づいて行動するので、本当は違う状況なのに、機械にその違いを入力していない(or機械が認識しない)場合は、同一の行動を取るしかなくなる。一方、方策ベースなら、その状況でも確率に基づくのでちゃんとゴールできる。
後悔(lt)
lt=E(V*-Q(at))
総後悔(Lt)
\(L_{t}=E\left[ \sum ^{t}_{\tau =1}V^{\ast }-Q\left( a_{\tau }\right) \right]\)
最高の一回の行動と実際の一回の行動との差の期待値
総報酬を最大化することは、総後悔を最小にすることと同値
探検(探査)
情報を集めること
ε-greedy法などによって知らない領域に踏み込むイメージ
利用
現時点でも情報を基にベストな選択をすること
探索と利用のジレンマ
暫定で1番報酬が多い選択をしたいが、長い目で見れば暫定1位以外の方法を試した方がよさそう、というもの。
実生活で言うと
探検:新しい飲食店に行く・新しい広告を表示する
利用:お気に入りの飲食店に行く・一番上手く行っていた広告を使う
ミニマックス手続き
相手が最善手を選ぶ場合に、自分側の損失が最小にする選択をする手続き
アルファベータ手続き
適切に用いれば、ミニマックス手続きよりも少ない子接点(データ数みたいなものです)で完全に同じ解を見つけられる
確率関連の話
AIの話をするときによく出てくるので用語などをまとめました
*確率の記号について
命題a,bが同時に起きる確率はP(a∧b)と書き、
確率変数X,Yがどちらも起きる時はP(X,Y)と書くのが正式みたいです。
X,Yが独立ならP(X,Y)=P(X)P(Y)。
不確かさ
物理的な実験を2回行うと、全く同じ出力値にはならない。入力の多くが未知だったり、測定できなかったりするからだ。これが不確かさ。
不確かさは大きく2つに分けれる。
偶然的不確かさ
どれだけ多くの情報を集めても低減できない不確かさ。
それぞれのシステムに固有のそれがあると考えられている。
確率分布で表現するのが最適とされている(偶然を扱いますもんね)。
例えば、サイコロを振った結果や放射性崩壊(シュレディンガーの猫、のやつですね)など。
認識論的不確かさ
理論的には知ることができるが、現時点では入手できない情報があるせいで生じる不確かさ。
なので、正しい情報を入手できればこの不確かさは低減できる。
実際は、費用や入手困難だったりして提言できないことが多いらしい。
例えば、製造寸法や負荷のばらつき、材料特性などがある。
ただ、偶然性不確かさに関しても「わかりません」で終わるのは面白くないので、人間は不確かさを「定量化」(ざっくり数える)をしようとする。
定量化
計算工学や実世界のシステムにおける不確かさを定量化すること。
統計的に要因の特性をはっきりさせ、観察結果を列挙しそこから法則を推論するモデルを作る。
変化しうる入力範囲があるとき、出力がどうなるかを考慮する。
金融問題などに使われている。
推論
一般には既知の事を基に未知の事を予想すること。
確率の分野では、特定の観測事象e1,・・・,enが既知で、質問変数Xの確率分布P(X|e1,・・・,en)を計算すること。
条件付き独立性
元々は独立でないが、とある条件のもとでは独立になる性質。
例えば、3つの事象「腕が痛む」「骨折する」「ギプスをする」を考える。
「腕が痛む」と「ギプスをする」は独立ではない。(腕が痛いかどうかでギプスをする確率が変わる)
しかし、腕が痛くても骨折していなければギプスをすることはほぼ考えられない(もし違ったらすいません)。
よって、骨折しているかどうかが分かれば、その2つは独立している。
式で書くと、
P(腕痛∧ギプス|骨折)= P(腕痛|骨折)P(ギプス|骨折)
骨折してなければそりゃ独立なのはわかるけど、骨折してても独立???って思いますが、実際に値を適当に設定して計算すると両辺が一致することがわかります。
列挙による推論
\begin{aligned}
P\left( X| e_{1},\ldots ,e_{n}\right) \\
=\alpha P\left( x,e_{1},\ldots ,e_{n}\right) \\
=\alpha\sum_{Y_1,\ldots,Y_{m}}P( X,e_{1},\ldots ,e_{n},Y_{i},\ldots,Y_{m})
\end{aligned}
αは正規化定数と呼び、「骨折」の計算でいうとP(骨折|腕痛)=αP(骨折∧腕痛)の場合はα=1/P(腕痛)である。
ベイジアンネットを使ってP(X, e1,・・・,en , Y1, ・・・, Ym)を求めて、P(X|e1,・・・,en)を計算する。
ベイジアンネット
完全結合確率分布を表現する確率変数間の依存関係を表す非循環有向グラフ。
確率分布
離散確率変数の全ての値をまとめて表現したもの。
weather(離散確率変数):値は晴れ、曇り、雨のどれかとすると、
| weather | P(weather) |
| 晴れ | 0.6 |
| 曇り | 0.3 |
| 雨 | 0.1 |
結合確率分布
複数の確率変数を並べて全ての組み合わせを表したもの。
coin(確率変数):値は表、裏のどっちかとすると、
| weather | coin | P(weather, coin) |
| 晴れ | 表 | 0.3 |
| 曇り | 表 | 0.15 |
| 雨 | 表 | 0.05 |
| 晴れ | 裏 | 0.3 |
| 雨 | 裏 | 0.15 |
| 曇り | 裏 | 0.05 |
完全結合確率分布
全ての確率変数に対する結合確率分布
※連続確率変数がある場合は表にできないので、確率密度関数というものを使って表現する。
ベイズの定理(ベイスの法則)
\(P\left( A| B\right) =\dfrac{P\left( B| A\right) P\left( A\right) }{P\left( B\right) }\)
事象 A が起こったという条件のもとで事象 B が起こる確率 P(B|A)を使って
、事象 B が起こったという条件のもとで事象 Aが起こる確率 P(A|B)を求めている。
マルコフ決定過程
1つ前の状態のみによって次の状態が決まる性質
これだと行動の報酬などが計算しやすい。
マルコフモデル
複数の内部状態があり、その状態が確率的に遷移するシステムで、現在の状態だけで次どこに遷移するかが決まる(これを、マルコフ過程に従う と言ったりする)。
入力の分布の時間発展を予想するモデル。
イオンチャネルや人口分布推移などに使われている。
隠れマルコフモデル
マルコフモデルに、観測されない(隠れた)状態を加えた確率モデル。
出力(観測された記号系列)の背後に存在する(隠れた)状態系列を推測することを目的に使う。
例えば、どこか遠いところに住んでいる友達がその日の活動報告をしてくれるとする。活動報告とは「長距離散歩した」「短距離散歩した」「散歩しなかった」の3種類のみ。その人が住んでいる場所の天気は教えてくれないが、「晴れ」「曇り」「雨」の3種類しかない。ただし天気はマルコフ過程に従う(前日の天気だけでその日の天気が決まる)とする。
晴れの時は長距離散歩する確率が0.5
曇りの時は、、、、
のような情報が与えられていると、その友達の報告(観測された記号系列)によって、その場所の天気(観測されない・隠れた状態)をある程度の確率で予測できます。
現実の例としては、言語の品詞を推定するのにこのモデルが使われます。
文章(観測された記号系列/友達の報告)
品詞(観測されない・隠れた・推測したい状態/天気)
の関係ですね。
信念
事象の確率がどれくらいか。(仮説をどれくらい信じているか)
データが追加されると更新される。
信念の更新はベイズ更新ともいう。
ベイズ更新
実は日常的に行なっています。
雲が分厚いから傘持って行こう、今日は猛暑だからアイスをいつもより多く仕入れよう、とか。
| データ | ||
| 仮説 | 傘を持っている | 傘を持っていない |
| 雨が降る | 0.20 | 0.80 |
| 雨が降らない | 0.10 | 0.90 |
事前確率として雨が降る確率が0.20とすると(傘とかAさんは関係なく、そもそも雨が降る確率)
| データ | ||
| 仮説 | 傘を持っている | 傘を持っていない |
| 雨が降る | 0.04 | 0.16 |
| 雨が降らない | 0.08 | 0.72 |
| total | 0.12 | 0.88 |
Aさんが「私は傘を持っています」と言うと
| データ | ||
| 仮説 | 傘を持っている | 傘を持っていない |
| 雨が降る | ? | 0 |
| 雨が降らない | ? | 0 |
| total | 1 | 0 |
この「?」の部分を求めるのがベイズ更新です。
雨が降る確率は
P(雨|傘)
=P(傘|雨)P(雨)/P(傘)
=0.20・0.20/0.12
=1/3
雨が降らない確率は(求めなくても1 – 1/3でいいですが、一応)
P(not雨|傘)
=P(傘|not雨)P(not雨)/P(傘)
=0.10・0.80/0.12
=2/3
| データ | ||
| 仮説 | 傘を持っている | 傘を持っていない |
| 雨が降る | 0.33 | 0 |
| 雨が降らない | 0.67 | 0 |
| total | 1 | 0 |
雨が降る確率、どれくらいの確率で雨が降るか信じるか、つまり信念が20%から33%に更新されました。
アルゴリズム紹介1パーティクルフィルタ(逐次モンテカルロ法)
確率分布による時系列データの予測手法。
現状態から遷移しうる複数の状態を、複数のパーティクル(粒子)で表現する。
状態価値関数(状態がsであるときに、エージェントが受け取る総報酬の期待値)の推定をしているが、方策評価や方策改善はしていない。
Input
時刻 t-1 におけるパーティクルの集合\(\chi_{t-1} = {x^1_{t-1}, x^2_{t-1},\ldots, x^M_{t-1}} \)
時刻 t における制御\(u_t\)
時刻 t における計測\(z_t\)
output
時刻 t におけるパーティクルの集合\(\chi_{t} = {x^1_{t}, x^2_{t},\ldots, x^M_{t}} \)
アルゴリズム部分
一時的にだけ使う仮の集合\(\bar{\chi_t}\)を空に初期化する
時刻 t におけるパーティクルのセット\(\chi_t\)を空に初期化する
for m=1,2,・・・,M do(サンプリングステップ)
状態に対する仮説\(x^m_{t}\)をサンプリング:\(x^m_{t}\)〜\(p(x_i | x^m_{t-1}, u_t\)
仮説\(x^m_{t}\)に対する重みの計算:\(w^m_t = p(z_t|x^m_t)\)
\(\bar{\chi_t}\)に\(x^m_{t}\)と\(w^m_{t}\)ペアを追加
end for
for m=1,2,・・・,M do
重み\(w^i_t\)に比例する確率で、インデックスi(1≦i≦M)(重みの計算ステップ)
\(\chi_t\)に\(x^i_t\)を追加(リサンプリングステップ)
end for
解説
このアルゴリズムはサンプリング・重みの計算・リサンプリングの3つのステップに分けられる。
サンプリングステップ
時刻 t-1 の各パーティクル\(x^m_{t-1}\)が処理される。
\(x^m_{t-1}\)と制御\(u_{t}\)から、状態遷移確率\(p(x_i | x^m_{t-1}, u_t\)に基づき、時刻 t の状態の仮説\(x^m_{t}\)がサンプリングされる。\(p(x_i | x^m_{t-1}, u_t\)を使ったサンプリングは、\(x^m_{t-1}\)に制御\(u_{t}\)を反映させた後にノイズを適用するという順方向(時間が進む方向)の計算なのでやりやすい。
重み計算のステップ
サンプリングで生成された仮説\(x^m_{t}\)についての重み\(w^m_{t}\)が計算される。
状態が\(x^m_{t}\)にある時、重み\(w^m_{t}\)は\(z_{t}\)が観測される確率密度(計測確率)\(p(z_t | x^m_t)\)となる。
仮説\(x^m_{t}\)に対応する重み\(w^m_{t}\)は、一時的なパーティクルフィルタの集合\(\bar{\chi_t}\)に保持される。
リサンプリングステップ
一時的な集合\(\bar{\chi_t}\)から、重複を許してM個のパーティクルを選択し、パーティクルの集合\(\chi_t\)を構成する。
この時、\(\bar{\chi_t}\)に含まれるパーティクル\(x^i_t\)が選択される確率は、そのパーティクルに対応する重み\(w^i_t\)に比例する。
リサンプリングする前のパーティクルの集合\(\bar{\chi_t}\)は、事前信念(事前確率・サンプリングする前の状態においてパーティクルxtが選ばれる確率を算出している)\(\bar{bel}(x_t\))の近似表現となっている。
重みに比例してサンプリングするので、最終的なパーティクルの集合\(\chi_t\)は、事後信念(事後確率・「重みに比例して確率が決まる」という情報が追加されたので、「もし\(x^i_t\)が選ばれたとしたら、計測の確率\(z_t\)のはどうなるか」という条件付き確率\(p(z_t|x^i_t)\)のことになる)\(bel(x_t)= np(z_t|x^m_t)\bar{bel}(x_t) \)に従って分布する。
重みの大きいパーティクルは、M回のサンプリングで何回も選ばれやすいので、\(\chi_t\)には、大抵重複したパーティクルがある。
重みが小さいと、1回も選ばれずに\(\chi_t\)に含まれないこともしばしば。
リサンプリングは、計測\(z_t\)を信念分布に反映させる操作と見れる。
\(\chi_t\)に含まれるパーティクルは、重み付きサンプリングによって分かる計測確率\(p(z_t|x_t)\)(事後信念bel(xt) )が大きいパーティクルだけに限定して計算すれば良い。なので、その状態の時の仮説の中で可能性が高いものだけに限定すれば、効率的に計算できる。
アルゴリズム紹介2Q学習
Q学習は解説済みなので、ここはあっさり書きます。
Q(s,a)を初期化(例えば0にする);
repeat (全エピソードに対して){
状態sを初期化;
while(sが終端状態でない){
Qから導かれる方策に従い状態sでの行動aを選択する;
行動aを取り、報酬と次状態r, s’を観測する;
最大値\(max_a’Q(s’, a’)\)を探す;(全てのa’に対してQ(s’, a’)のテーブルを検索してピックアップする)
\(Q\left( s, a\right) \leftarrow Q\left( s,a\right) \
+\alpha( r+\gamma \max_{a’}Q\left( s’,a’\right) \
-Q\left( s,a\right) )\);(価値を更新)
\( s \leftarrow s’\);(状態遷移)
}
}
将棋はチェスよりも難しい?
将棋には「持ち駒」や「成る」システムがある分、チェスよりも考慮する要素が多い。
なのでAIに学習させる手間が多くなるので難しいと言える。囲碁は盤面が大きいので計算がより膨大になり難しくなると言われます。(人間にとってもそうかもしれませんね)
また、ポーカーのような不完全情報ゲーム(運が関わるゲーム)もソフトフェアが勝ちにくくなります。ゲームの状況を完全に把握できない(ポーカーなら相手の手札がわからない、など)部分がソフトウェアの勝利を難しくしている。
完全情報ゲームの複雑さ順:三目並べ<チェッカー<チェス<中国象棋<五目並べ<囲碁
※ゲーム木と状態空間の複雑性を参考にしている
不完全情報ゲームの情報数の順番:1対1テキサスホールデム(制限付)<1対1テキサスホールデム(無制限)<ブリッジ<麻雀
*情報集合数と集合の平均的な大きさを参考にしている
参考文献
パーティクルフィルタ(pdf)
https://sterngerlach.github.io/doc/particle-filter.pdf
星の本棚
https://yagami1https://yagami12.hatenablog.com/entry/2019/02/22/210608
知識工学の公開講義資料(愛媛大学)
http://aiweb.cs.ehime-u.ac.jp/~ninomiya/ke/
統計的モデリング基礎⑩〜ベイズモデリング〜
https://hkashima.github.io/FSM2018_10.pdf
deepmind社の公式サイト
https://www.deepmind.com/learning-resources/introduction-to-reinforcement-learning-with-david-silver
制御工学の基礎あれこれ
http://arduinopid.web.fc2.com/N63.html
最後に
最後まで読んだ人は猛者ですね。
いい意味で変人です。誇りに思ってください。
機械学習の記事を書いているはずが、ところどころ「これって人間にも当てはまるよな、、、」と思わされる部分がありました。
間違っている部分があればコメントで教えてくださいorz







コメント