どうも!こんにちは。カサニマロです。
今日の問題はこちら!
1辺9cmの豆腐(立方体)1個を1辺3cmの立方体27個に包丁で切り分けるには最低でも何回切り分ける必要があるか?
切り分けた豆腐を重ねたりするのはokですが、切っている途中で包丁の向きを変えることはできないとします。
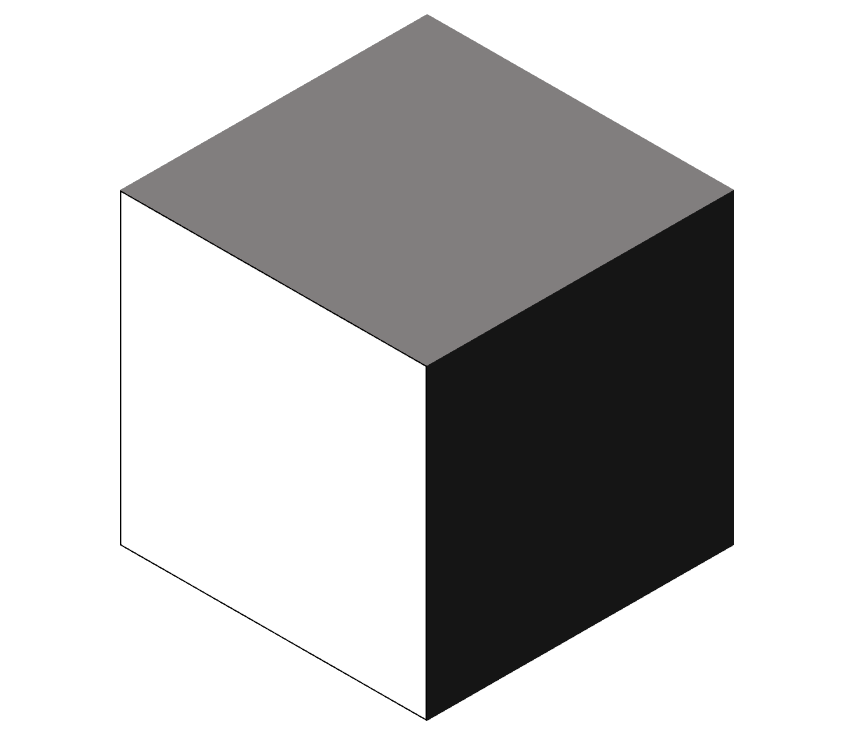
思考のポイントとしては、「絶対にこの1辺3cmの立方体が生まれないと、27等分できない」というポイントを探ることです。
まず、問題の「1辺9cmの立方体」を大きな立方体、「1辺3cmの立方体」を小さな立方体と名づけることにしましょう。
それでは、第一ステップとして、小さな立方体が完成する過程を想像してみることにしましょう。
問題文では、大きな立方体から、27個の小さな立方体を切り離していくという状況を想定していますが、ここでは、十分に大きなカタマリから、小さな立方体を1つだけ切り離していく状況を想定してみましょう。
絵ではわかりにくいので、言葉で理解していきましょう。
例えるなら、バカでかい豆腐から、ど真ん中の小さいブロックを掘削するイメージです。
この小さいブロックは立方体ですから、ちょうどサイコロのような形状をしており、面が6つあることが確認できますね(サイコロの目は1~6の6つですよね)。
ここで、ど真ん中の小さいブロックの目線になってみます。今、あなたはど真ん中の小さいブロックです。
「すー-」っと音がし始めて、まず自分の上部(あたま)がスライスされることがわかります。これで1面。
次に下部(足もと)。これで2面。
それから、右側面(右半身)。これで3面。
ここで、左側面(左半身)。これで4面。
そして、後ろ側(背中)。これで5面。
最後に、前(お腹の面)。これで6面。
――はい。あなたは、サイコロになっちゃいました。
以上のような観点で考えてみますと、大きな立方体から、27個の小さな立方体を切り離していくという状況についても、ど真ん中の小さな立方体が完成するとき、同時にその上下左右前後のブロックも芋づる式に切り離され、ちゃんとすべてが切り離されたということになります。
つまり、6回というのが正解っぽそうです。
ここで、6回が本当に最小の回数なのかという疑問についてなのですが、そもそも真ん中のブロックの面が6つですから、5回以下のスライスで掘削することができません。
したがって、
6回
結論、真ん中の3cm角のブロックに注目すればいいわけです。
面が6面あるので、真ん中の3cm角のブロックを切り出すには6回は切らないといけないことが分かる。
それだけの問題でした!







コメント