どうも!こんにちは。カサニマロです。
皆さん元気ですか。
今日も一日頑張りましょう~。

因数分解って何なんだろう??
今回は高校1年生で学ぶ因数分解についてまとめていきます。
因数分解は、今後数学を勉強していく中で頻繁に用いていくものなので必ず覚えておいた方が良いでしょう。
ここでつまずく人も多いのではないでしょうか?
そんな因数分解についてやり方を詳しく説明していきます。
- 因数分解とは何なのか?
- 因数分解について知ろう!
- たすきがけのやり方
- たすきがけをマスターしよう!
- 簡単な因数分解の覚え方
- 因数分解の公式を語呂合わせを混じえながら覚えよう!
- 因数分解関連の問題集
- まとめ
因数分解とは何なのか?
因数分解とは、下記の式のように和や差の式で表されている式を、積の式に変形することを意味します。
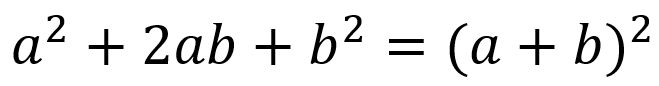
逆に、積の式を和や差の式に変形することを展開といいます。上記の式の右辺と左辺を反対にしたものが展開になります。
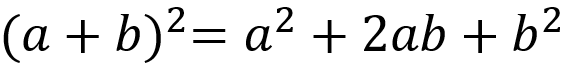

つまり、「+」や「ー」の記号を使わずに、掛け算の集まりにする作業のことを、因数分解というんだね!
展開は中学の時の記憶でなんとなくわかるかな?
ここでは、因数分解と展開が逆の作業ということを抑えておくといいでしょう!
これらの因数分解や展開はこれからの数学を勉強していく中で頻繁に使っていくものなのでしっかり覚えていきましょう!
たすきがけのやり方
まずは、たすきがけを用いた因数分解のやり方を覚えていきましょう。
基本的に簡単な因数分解はたすきがけを用いて解けることが多いです。
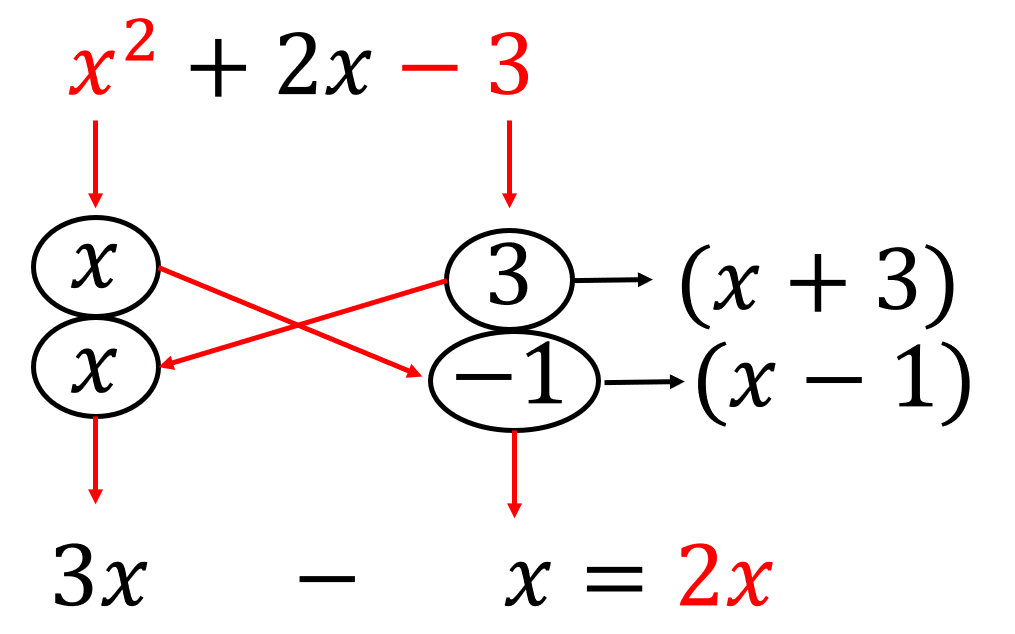
例えば、下記の式をたすきがけで因数分解する場合、始めと終わりの項(赤い部分)に注目します。
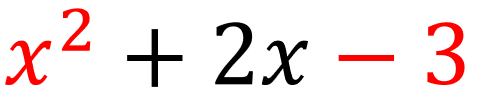
赤い部分はx2とー3ですね。
ここで、「何と何を掛け算するとx²になるか」「何と何を掛け算すると-3になるか」を考えます。
下の式のようにですね。
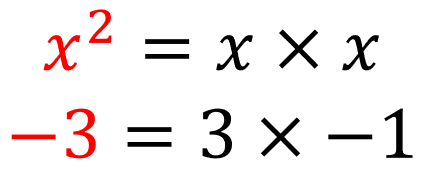
これらを下記に示すように書き出します。
結論としては、赤線の斜め矢印の間を掛け合わせたものの和がもとの式の真ん中の項と同じなら、たすきがけが成功しています(あ、まだわかんなくていいよ)
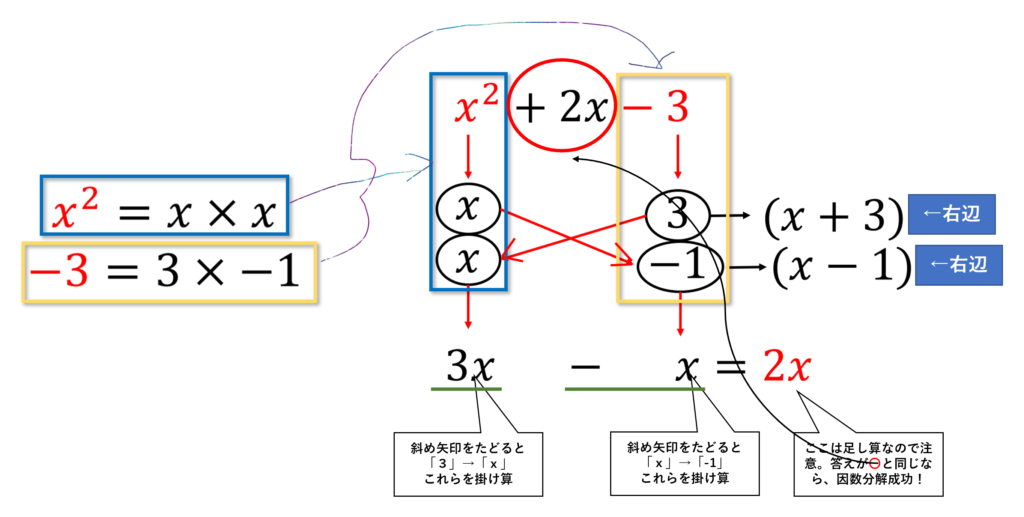
もう少し、図解してみることにします。ちょっと見づらいですが、頑張って理解してみてください。
これより因数分解の結果は、下記に示すようになります。
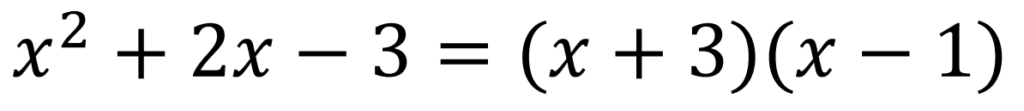
たすきがけは他の問題にも適用することができ、汎用性が高い解き方になっています。
ただし、教科書や参考書、ブログといった動きのない媒体では理解が難しい場合もあるので、こういった手順が複雑な問題については、YouTubeなどの動画で理解を試みるのをお勧めします。
簡単な因数分解の覚え方
次に因数分解の公式の覚え方について説明していきます。
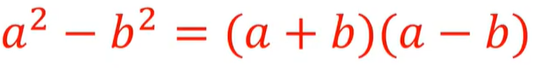
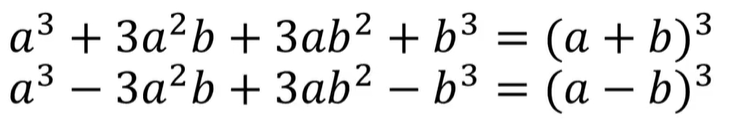
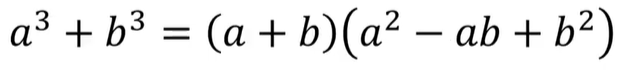
一番上の式はたすきがけでも解くことができないわけではないのですが、覚えてしまったらすぐに解けるようになるので時間短縮のためにも覚えておいて損はないと思います。
それ以外の式は覚えておかないと問題が解けないことがあるため覚えておきましょう。
動画で公式を語呂合わせを用いながら覚えていきましょう!例題も用いながら実際の問題での応用の仕方なども学べる内容になっています。
この動画を見ることで上記の公式を用いた因数分解が誰でもできるようになります!
因数分解関連の問題集
まとめ
今回は、高校1年生で習う因数分解のやり方を動画を交えながら説明していきました。
因数分解の解き方は、たすきがけと公式を用いたものがあり、これらを使うことで基本的には因数分解できると思います。
この記事が因数分解の理解の助けになれば幸いです。










コメント