どうも!カサニマロです。
今日の問題はこちら!
今日の問題


ヒントおじさん
やっぱり、こういう直接解きにくい問題は、aの式としてまとめてみたいね!
ひとまず、分母を3つともそろえるのは大事でしょうね。
ということで、、、
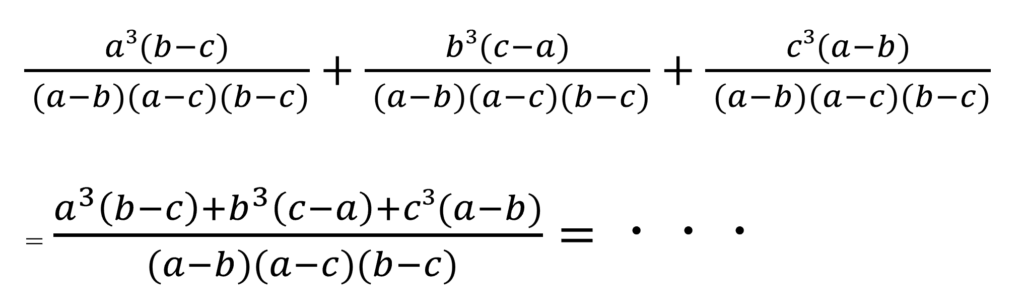
なんか、こういう風に変形していくんだろうなぁ、ということは検討が付きます。
しかし、僕らは気づきます。「ああ、分子だけいじっていけばいいんだな・・・」と。
そこで、もっと賢い方法(記述量を少なくする方法)として、以下の解法を本ブログでは記します。
【解答・解説】
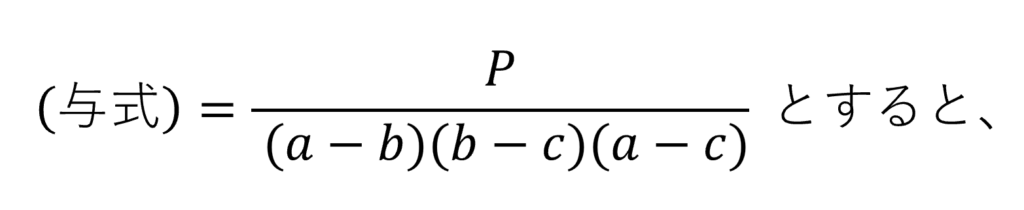
P=a³(b-c)+b³(c-a)+c³(a-b)
=(b-c)a³ – (b³-c³)a + bc(b²-c²) ←a³の係数、a²の係数[今回はなし=0]、aの係数、定数項を際立たせる形に変形
=(b-c){a³-(b²+c²+bc)a+bc(b+c)} ←b³-c³の因数分解、b²-c²の因数分解を適用
このb-cの部分を見て、(a-b)(a-c)も出るのが検討つきますね。なぜなら与式が対称的なので、因数分解形も対称的である可能性が高いからです。
=(b-c){a²-(b+c)a+bc}{a+(b+c)}
(ここは因数定理でいけちゃいますが、もし難しそうであれば上記の予想をもとに、下記の式から逆算して埋めていく形でもいいんじゃないかとは思います!)
=(b-c)(a-b)(a-c)(a+b+c)
よって、(与式)= a+b+c








コメント