y3 = x2 – 4 (x,yは自然数)の時、yは奇数でないことを示せ
- ヒント1
背理法で示す - ヒント2
偶奇に注目
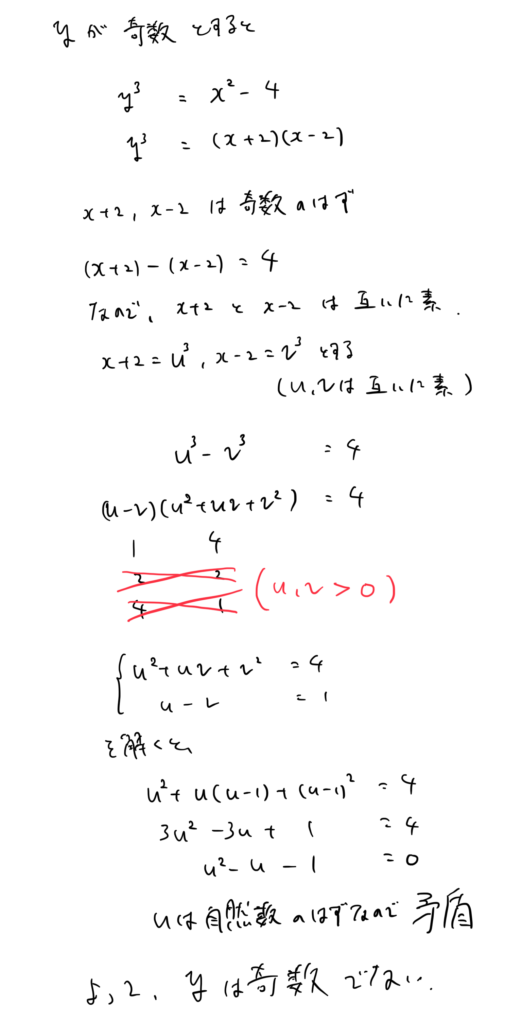
出てきた内容(技術?)としては
・背理法
・因数分解
・奇数z と z+4が互いに素(互除方すれば、gcd(z,z+4) = gcd(z,4)=1 )
・「いい感じに」文字で置く(x+2=u3 とおいたのは、u3 と3乗があれば因数分解ができる→因数分解すれば式が絶対ではないが式が都合良く変形して仮定と矛盾する形になるだろう→矛盾すれば背理法で終了)
の4つですね。(もちろん、実際に問題を解くときは、「え〜、今回使う技術は何個だ?」とか気にしません。解説のために書いているだけです。)
実際の思考の流れは
「右辺は因数分解できるな」
「yが奇数でないのを示すのか〜〜、奇数だと仮定して、何か偶奇利用しつつ因数分解していけば、矛盾見つけて背理法でいけるんじゃね」
って感じでしょうか。
もちろんこんなに最小限の思考じゃなくて紆余曲折しながら見つけるパターンが多いでしょう。
普通、テストでも入試でもこのような大問なら数十分くらいは時間かかる前提で問題が作られているでしょうから。








コメント